บทความ
นลพรรณ มณีโชติ
ลักษณะของเส้นอัตราผลตอบแทนกับนโยบายการคลังของประเทศไทย
Yield Curve Characteristics pertaining to the Fiscal Policy of Thailand
1. บทคัดย่อ
การศึกษานี้ได้ศึกษาเกี่ยวกับลักษณะของเส้นอัตราผลตอบแทน ประกอบด้วย (1) ระดับ (2) ความชัน และ (3) ความโค้ง ซึ่งเป็นปัจจัยแฝง (Latent Factors) โดยใช้วิธี Nelson and Siegel (1987) และการประมาณค่า Maximum Likelihood ด้วย Kalman Filter จากนั้นจึงนำปัจจัยแฝงข้างต้นไปใช้คำนวณหาความสัมพันธ์เชิงพลวัตระหว่างลักษณะของเส้นอัตราผลตอบแทนกับนโยบายการคลังของประเทศไทยด้วยการวิเคราะห์แบบจำลอง VAR และ Impulse Response Functions ผลการศึกษาพบว่าการดำเนินนโยบายการคลังผ่านการก่อหนี้สาธารณะ ส่งผลต่อการเปลี่ยนแปลงระดับ ความชัน และความโค้งในทิศทางเดียวกัน สอดคล้องกับทฤษฎีและผลการศึกษาจากการทบทวนวรรณกรรมที่เกี่ยวข้อง นอกเหนือจากนโยบายการคลัง อัตราเงินเฟ้อเป็นตัวแปรที่สำคัญที่สุดในการอธิบายลักษณะทั้งสามของเส้นอัตราผลตอบแทนโดยเปรียบเทียบกับ VIX และ GDP Growth ผลการศึกษาสามารถนำไปใช้คาดการณ์ผลกระทบของการดำเนินนโยบายการคลังที่มีต่อภาคเศรษฐกิจจริง ผ่านการวิเคราะห์สัญญาณข้อมูลการเปลี่ยนแปลงลักษณะเส้นอัตราผลตอบแทนในตลาดพันธบัตรรัฐบาล
2. บทนำ (Introduction)
พันธบัตรรัฐบาลถูกจัดว่าเป็นสินทรัพย์ปลอดภัย (Safe Asset) เนื่องจากมีความเสี่ยงจากการผิดนัดชำระหนี้ที่ต่ำหรือเป็นศูนย์ แต่อาจมีความเสี่ยงอื่น ๆ เช่น ความเสี่ยงจากอัตราดอกเบี้ยหรือภาวะเงินเฟ้อ ด้วยเหตุผลดังกล่าวทำให้การเคลื่อนไหวของอัตราผลตอบแทนพันธบัตรรัฐบาล (Bond Yield) ขึ้นอยู่กับสถานการณ์และเงื่อนไขทางเศรษฐกิจที่จะเกิดขึ้น การเคลื่อนไหวของ Bond Yield จึงมีความสำคัญและสามารถบ่งบอกถึงภาวะเศรษฐกิจในบางช่วงได้ และ Bond Yield ยังถูกจัดให้เป็นอัตราที่ใช้สำหรับเทียบเคียง (Benchmark) ให้กับตราสารหนี้อื่น ๆ โดยเมื่อเปรียบเทียบกับหุ้นกู้เอกชน (Corporate Bonds) หรือสินทรัพย์ทางการเงินอื่น ๆ แล้วมีความเสี่ยงมากกว่าหลักทรัพย์ของรัฐบาล เนื่องจากบริษัทจะมีความเสี่ยงเฉพาะตัว (Idiosyncratic Risk) เช่น ความเสี่ยงที่เกิดจากการบริหารจัดการภายใน ปัญหาทางการเงินหรือปัจจัยอื่น ๆ ที่ส่งผลต่อผลประกอบการของบริษัท ทำให้บริษัทมีโอกาสที่จะผิดนัดชำระหนี้ให้กับผู้ถือหุ้นกู้ได้ ดังนั้น การที่ Bond Yield มีความสัมพันธ์กับการเปลี่ยนแปลงของเงื่อนไขทางเศรษฐกิจ ในภาวะปกติ Bond Yield ระยะยาวจะมากกว่า Bond Yield ในระยะสั้น เพื่อชดเชยความเสี่ยงจากการลงทุนและอัตราเงินเฟ้อในอนาคต เส้นอัตราผลตอบแทน (Yield Curve) จึงมีลักษณะแบบปกติหรือเป็นบวก (Normal Yield curve) ในทางกลับกันหากเศรษฐกิจอยู่ในภาวะไม่ปกติ เช่น นักลงทุนมีมุมมองที่เป็นลบต่อภาวะเศรษฐกิจ ณ ขณะนั้น โดยคาดว่าจะเกิดภาวะเศรษฐกิจตกต่ำ จึงทำให้นักลงทุนคาดการณ์ว่าธนาคารกลางจะใช้นโยบายการเงินแบบขยายตัวด้วยการลดอัตราดอกเบี้ยนโยบาย ส่งผลให้เกิดความกังวลว่าเศรษฐกิจระยะสั้นจะเกิดความผันผวนและไม่แน่นอนจึงทำให้นักลงทุนจำนวนมากหันไปซื้อพันธบัตรระยะยาวเพิ่มขึ้น ส่งผลให้ Bond Yield ระยะยาวปรับตัวลดลง ในขณะที่ Bond Yield ระยะสั้นปรับตัวสูงขึ้น เนื่องจากอุปสงค์ของพันธบัตรระยะสั้นน้อยลง ส่งผลให้ Yield Curve เป็นแบบลาดลง (Inverted Yield Curve)
การเปลี่ยนแปลงลักษณะของ Yield Curve อาจเกิดมาจากหลายสาเหตุ ซึ่งจากการศึกษาทฤษฎีที่เกี่ยวกับนโยบายการคลัง รวมถึงการศึกษาอื่น ๆ ที่เกี่ยวข้องพบว่าการเปลี่ยนแปลงลักษณะของ Yield Curve มีการเปลี่ยนแปลงใน 3 รูปแบบ ได้แก่ การเปลี่ยนแปลงระดับ การเปลี่ยนแปลงความชัน และการเปลี่ยนแปลงความโค้ง การศึกษาเกี่ยวกับ Yield Curve ส่วนใหญ่จะมีการศึกษาเกี่ยวกับการดำเนินนโยบายการเงินส่งผลต่อ Yield Curve และมีการศึกษาเกี่ยวกับการดำเนินนโยบายการคลังส่งผลต่อ Yield Curve ค่อนข้างน้อย โดยเฉพาะในเอเชีย อย่างไรก็ตาม ในช่วงปี 2008 – 2010 สหรัฐและประเทศในยุโรปได้มีการศึกษาเกี่ยวกับการดำเนินนโยบายการคลังส่งผลต่อ Yield Curve ค่อนข้างมาก เนื่องจากในช่วงเวลานั้นนโยบายการคลังมีความสำคัญในเรื่องของการก่อหนี้สาธารณะและเพิ่มรายจ่ายภาครัฐ เพื่อกระตุ้นเศรษฐกิจในช่วงเวลาดังกล่าว นำมาสู่ความสนใจที่จะศึกษาเกี่ยวกับการดำเนินนโยบายการคลังส่งผลต่อลักษณะของ Yield Curve ของประเทศไทย เนื่องจากในปัจจุบันประเทศไทยเริ่มมีการก่อหนี้สาธารณะในปริมาณที่ใกล้เคียงกับสหรัฐในช่วงเวลานั้น และเริ่มมีลักษณะของ Yield Curve ที่เปลี่ยนแปลงไปจาก Normal Yield Curve เป็นแบบราบ (Flat Yield Curve) และมีแนวโน้มที่จะเป็น Inverted Yield Curve ได้ในอนาคต จึงมีวัตถุประสงค์เพื่อการศึกษา ดังนี้ (1) ศึกษาเกี่ยวกับลักษณะของ Yield Curve ประกอบด้วย ระดับ ความชัน และความโค้ง (2) เพื่อศึกษาความสัมพันธ์เชิงพลวัตระหว่างลักษณะของ Yield Curve กับนโยบายการคลังของประเทศไทย และ (3) เพื่อนำผลการศึกษาไปใช้ประโยชน์ในการเสนอแนะเกี่ยวกับการนำ Yield Curve มาพิจารณาร่วมกับการวางแผนการดำเนินนโยบายการคลังต่อไป
3. ทฤษฎีและวรรณกรรมที่เกี่ยวข้อง (Theories and related literature)
นโยบายการคลังมีบทบาทสำคัญในการกำหนดทิศทางเศรษฐกิจและตลาดทางการเงิน นอกจากนี้ นโยบายการคลังยังมีผลกระทบต่อ Yield Curve โดยนโยบายการคลังแบบขยายตัวจะทำให้ Yield Curve มีการเปลี่ยนแปลงระดับและความชันเพิ่มขึ้นในระยะยาว อย่างไรก็ตาม ปัจจัยอื่น ๆ ก็อาจส่งผลกระทบได้ เช่น หากนักลงทุนมีความกังวลว่าเศรษฐกิจจะไม่ดี จึงไปซื้อ Safe Asset หรือ Flight to Safety ก็มีบทบาทสำคัญในการเปลี่ยนแปลงของ Yield Curve เช่นกัน ทั้งนี้ การคาดการณ์ของนักลงทุนอาจสอดคล้องกับทฤษฎีต่าง ๆ ดังนี้ (1) Expectations Theory เป็นทฤษฎีที่ใช้อธิบายว่าอัตราดอกเบี้ยระยะยาวจะถูกกำหนดโดยการคาดการณ์ของตลาดเกี่ยวกับอัตราดอกเบี้ยระยะสั้นในอนาคต ทฤษฎีนี้ระบุว่าเมื่อมีการประกาศการเปลี่ยนแปลงนโยบายการคลัง การเปลี่ยนแปลงความคาดหวังเกี่ยวกับภาวะเศรษฐกิจในอนาคตจะเกิดขึ้น เช่น นโยบายการคลังแบบขยายตัวอาจทำให้นักลงทุนคาดหวังว่าการเติบโตทางเศรษฐกิจจะขยายตัว ซึ่งอาจทำให้อัตราผลตอบแทนระยะยาวสูงขึ้น นอกจากนี้ การเปลี่ยนแปลงนโยบายการคลังอาจส่งผลกระทบทันทีต่ออัตราดอกเบี้ยระยะสั้น เช่น หากรัฐบาลเพิ่มการใช้จ่ายภาครัฐเพื่อตอบสนองต่อภาวะเศรษฐกิจตกต่ำ อาจส่งผลให้อัตราดอกเบี้ยระยะสั้นสูงขึ้น เนื่องจากรัฐบาลแข่งขันกับผู้กู้ยืมรายอื่น อาจส่งผลให้อัตราผลตอบแทนระยะสั้นเพิ่มขึ้นเร็วกว่าอัตราผลตอบแทนระยะยาว และ (2) Liquidity Premium Theory เป็นทฤษฎีนี้พัฒนามาจาก Expectations Theory กล่าวคือ อัตราดอกเบี้ยของพันธบัตรรัฐบาลระยะยาวจะเท่ากับค่าเฉลี่ยของการคาดการณ์อัตราดอกเบี้ยระยะสั้นบวกด้วยส่วนชดเชยความเสี่ยงจากสภาพคล่อง (Liquidity Premium) ซึ่งส่วนชดเชยสภาพคล่องที่บวกเพิ่มขึ้น คืออัตราผลตอบแทนที่นักลงทุนจะต้องได้รับเพิ่มขึ้น เนื่องจากอุปสงค์ในพันธบัตรแต่ละรุ่นอายุมีความแตกต่างกัน ทำให้มีความยากง่ายในการซื้อขายที่แตกต่างกัน
Zhe Huang (2019) ได้ศึกษาเกี่ยวกับ Yield Curve ของตั๋วเงินคลังและพันธบัตรรัฐบาลของสวีเดน โดยใช้แบบจำลอง Dynamics Nelson-Siegel พบว่าแบบจำลอง Dynamics Nelson-Siegel เป็นแบบจำลองที่เสถียรและสะดวกที่สุด เพื่อให้พอดีกับ Bond Yield ที่ครบกำหนด และแบบจำลอง Dynamics Nelson-Siegel มีข้อได้เปรียบในการประมาณการ Bond Yield ระยะกลางและระยะยาวได้ และ Jan Annaert, Anouk G.P. Claes, Marc J.K. De Ceuster and Hairui Zhang (2013) ได้ศึกษาเกี่ยวกับแบบจำลอง Nelson-Siegel ซึ่งจะช่วยให้สามารถรวมปัจจัยเพิ่มเติมที่มีอิทธิพลต่อลักษณะของ Yield Curve เช่น ตัวแปรทางเศรษฐกิจมหภาคหรือข้อมูลอื่น ๆ ของตลาด ด้วยเหตุนี้จึงกลายเป็นวิธีที่ใช้กันอย่างแพร่หลายและเป็นที่ยอมรับในการประมาณการและคาดการณ์ Yield Curve
Litterman and Scheinkman (1991) และ Diebold and Li (2006) ได้มีการศึกษาเกี่ยวกับลักษณะของ Yield Curve และตีความปัจจัยแฝงของ Yield Curve เป็นระดับ ความชัน และความโค้ง อีกทั้งได้มีการเสนอแนะ 2 ขั้นตอนในการประมาณค่าปัจจัยแฝง ดังนี้ (1) ประมาณค่าปัจจัยแฝงทั้งสามด้วยกำลังสองน้อยที่สุดที่ไม่เป็นเส้นตรง ซึ่งมีเงื่อนไขบางประการเกี่ยวกับการให้น้ำหนักของความชันและความโค้งในแต่ละช่วงอายุพันธบัตรรัฐบาล และ (2) ประมาณการปัจจัยเพื่อคาดการณ์ Yield Curve จะเห็นได้ว่าการวิเคราะห์ส่วนใหญ่ได้มุ่งเน้นไปที่ความสัมพันธ์ระหว่างปัจจัยแฝงของ Yield Curve กับนโยบายการเงิน อัตราเงินเฟ้อ และกิจกรรมทางเศรษฐกิจที่แท้จริง (Diebold, Rudebusch and Aruoba (2006), Carriero, Favero and Kaminska (2006), Dewachter and Lyrio (2006), Hordahl, Tristani and Vestin (2006), Rudebusch and Wu (2008) และ Hoffmaister, Roldós and Tuladhar (2010)) อาจอธิบายได้ด้วยข้อเท็จจริงที่ว่าแนวทางดังกล่าวเกี่ยวข้องอย่างใกล้ชิดกับวรรณกรรมมากมายที่เกี่ยวกับการใช้ Yield Curve ทั้งความชันและความโค้งในการคาดการณ์ความผันผวนของกิจกรรมทางเศรษฐกิจที่แท้จริง รวมถึงอัตราเงินเฟ้อเป็นหลัก (Ang, Piazzesi and Wei (2006) และ Rudebusch and Williams (2007)) ในขณะที่ Diebold, Rudebusch and Aruoba (2006) และ Carriero, Favero and Kaminska (2006) ได้ใช้แบบจำลอง Nelson-Siegel ในการแยกลักษณะ Yield Curve นอกจากนี้ วรรณกรรมที่กล่าวว่าหนี้สาธารณะ (Evans and Marshall (2007)) และการขาดดุลงบประมาณ (Dai and Philippon (2006)) มีส่วนช่วยในการอธิบายว่าปัจจัยใดที่เป็นตัวกำหนด Yield Curve ในขณะที่ผลกระทบของการใช้จ่ายภาครัฐต่อ Yield Curve ได้รับความสนใจน้อยกว่ามาก เนื่องจากความเชื่อมโยงระหว่างการใช้จ่ายภาครัฐและ Yield Curve นั้นยากต่อการวิเคราะห์เชิงประจักษ์ และมีวรรณกรรมที่สรุปว่าการใช้จ่ายของรัฐบาลมีผลกระทบเพียงเล็กน้อยต่อ Yield Curve (Evans and Marshall, 2007) ซึ่งเป็นผลลัพธ์ที่น่าประหลาดใจ เนื่องจากทฤษฎีเศรษฐศาสตร์คาดการณ์ว่าการใช้จ่ายของรัฐบาลที่เพิ่มขึ้นน่าจะนำไปสู่ความต้องการบริโภคโดยรวมที่เพิ่มขึ้น (Baxter and King, 1993) ซึ่งผลักดันให้อัตราดอกเบี้ยสูงขึ้น (Fisher and Turnovsky, 1992) จึงเป็นเรื่องที่น่าสนใจที่มีวรรณกรรมที่พยายามหาความสัมพันธ์ระหว่าง Yield Curve กับตัวแปรทางการคลังในแบบจำลองเชิงประจักษ์ของเศรษฐกิจ โดยการหาความสัมพันธ์เชิงพลวัตระหว่างตัวแปรทางการคลังที่ไม่ใช่การใช้จ่ายภาครัฐ เช่น หนี้สาธารณะต่อผลิตภัณฑ์มวลรวมภายในประเทศ (Debt-to-GDP Ratio) และดุลงบประมาณ (Budgetary Balance) โดยหาความสัมพันธ์กับลักษณะของ Yield Curve ซึ่งเป็นปัจจัยแฝง 3 ตัวแปร ได้แก่ ระดับ ความชัน และความโค้ง ที่ได้รับจากตัวกรองคาลมาน (Kalman Filter) ซึ่งจะถูกใช้ใน VAR พร้อมตัวแปรเชิงมหภาคและตัวแปรทางการคลัง โดย António Afonso and Manuel M.F. Martins (2012) ได้มีการวิเคราะห์ความสัมพันธ์ระหว่างระดับ ความชัน และความโค้งของ Yield Curve กับตัวแปรทางการคลัง ได้แก่ Debt-to-GDP Ratio และการขาดดุลงบประมาณในสหรัฐและเยอรมนี พบว่าการเพิ่มขึ้นของระดับของ Yield Curve มีความสัมพันธ์กับการเพิ่มขึ้นของ Debt-to-GDP Ratio ในขณะที่การขาดดุลงบประมาณ เพิ่มขึ้นมีความสัมพันธ์กับความชันของ Yield Curve ลดลง
3. ข้อมูลและวิธีการวิจัย (Data and Methodology)
การศึกษาครั้งนี้จะใช้กรอบการวิเคราะห์ตัวแปรเชิงมหภาคและเสริมสร้างแบบจำลองเชิงประจักษ์ของเศรษฐกิจโดยมีตัวแปรเศรษฐกิจมหภาค ได้แก่ GDP Growth (ร้อยละ) และ Inflation (ร้อยละ) และตัวแปรที่แสดงถึงนโยบายการคลัง ได้แก่ Debt-to-GDP Ratio (ร้อยละ) รวมถึงตัวแปรเพิ่มเติมที่เกี่ยวข้องกับปัจจัยทางการเงิน ได้แก่ ดัชนีความผันผวน (Volatility Index: VIX) ซึ่งคำนวณโดยตลาดซื้อขายอนุพันธ์ (Chicago Board Options Exchange: CBOE) เพื่อให้สามารถระบุผลกระทบจากการดำเนินนโยบายการคลังภายใต้ความผันผวนได้อย่างสมเหตุสมผล และได้ศึกษาเกี่ยวกับความสัมพันธ์เชิงพลวัตระหว่างตัวแปรทางการคลังกับลักษณะของ Yield Curve ประเทศไทย ซึ่งลักษณะของ Yield Curve จะวัดโดยการประมาณการของระดับ ความชัน และความโค้ง ของ Nelson and Siegel (1987) และการประมาณค่า Maximum Likelihood ด้วย Kalman Filter ที่แนะนำโดย Diebold and Li (2006) และ Diebold, Rudebusch and Aruoba (2006) วิเคราะห์ด้วยแบบจำลอง VAR แต่เนื่องจากการวิเคราะห์ VAR ไม่สามารถวิเคราะห์จากค่าสัมประสิทธิ์ได้ จึงต้องอาศัยวิธีอื่น อาทิ Impulse Response Function มาศึกษาการตอบสนองของตัวแปรในแบบจำลอง รวมถึงการประมาณค่า Variance Decomposition และการทดสอบ Granger Causality เพื่อให้ได้หลักฐานเชิงประจักษ์ที่แสดงว่าตัวแปรที่สนใจนั้นมีอำนาจการพยากรณ์ต่อกันอย่างไร โดยมีระเบียบวิธีวิจัย 2 ขั้นตอน ดังนี้
3.1 ปัจจัยแฝง (Latent Factors)
การหาปัจจัยแฝงซึ่งเป็นลักษณะของ Yield Curve จะถูกประเมินโดยการประมาณ Maximum Likelihood ด้วย Kalman Filter เช่นเดียวกับใน Diebold, Rudebusch and Aruoba (2006) และ António Afonso and Manuel M.F. Martins (2012) เนื่องจากปัจจัยแฝงของ Yield Curve นั้นไม่สามารถสังเกตได้แต่เป็นตัวแปรพื้นฐานที่มีบทบาทสำคัญในการกำหนดลักษณะและการเคลื่อนไหวของ Yield Curve โดยปัจจัยแฝงที่ใช้อธิบาย Yield Curve ได้แก่ (1) ระดับ (Level) แสดงถึงระดับโดยรวมของ Yield Curve แสดงลักษณะการเปลี่ยนแปลงของอัตราดอกเบี้ยที่สม่ำเสมอตลอดระยะเวลาครบกำหนด (2) ความชัน (Slope) อธิบายความแตกต่างของอัตราผลตอบแทนระหว่างระยะเวลาครบกำหนดในระยะสั้นและระยะยาว การเพิ่มขึ้นของความชันบ่งชี้ว่าอัตราระยะยาวเพิ่มขึ้นเร็วกว่าระยะสั้น ในขณะที่การลดลงของความชันบ่งบอกถึงสิ่งที่ตรงกันข้าม ความชันมักเชื่อมโยงกับความคาดหวังของตลาดเกี่ยวกับอัตราดอกเบี้ยในอนาคต โดยเฉพาะในระยะยาว และ (3) ความโค้ง (Curvature) แสดงถึงความนูนหรือความเว้าของ Yield Curve โดยความโค้งที่เพิ่มขึ้นบ่งชี้ว่าอัตราผลตอบแทนระยะกลางกำลังเปลี่ยนแปลงในอัตราที่แตกต่างจากอัตราผลตอบแทนระยะสั้นและระยะยาว ความโค้งอาจได้รับอิทธิพลจากปัจจัยต่าง ๆ รวมถึงความเชื่อมั่นของตลาดและความต้องการของนักลงทุน
การจำลอง Yield Curve โดยใช้รูปแบบของการประมาณส่วนประกอบแบบเอ็กซ์โพเนนเชียล (Three-Component Exponential Approximation) ที่เสนอโดย Nelson and Siegel (1987) ดังสมการที่ (1)
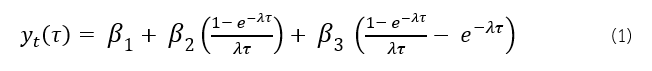


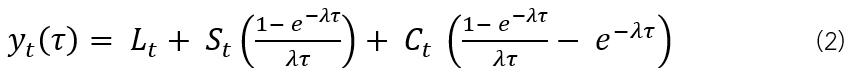

3.2 แบบจำลอง Vector Autoregressive (VAR)
ตัวแปรที่ใช้ในการหาความสัมพันธ์กับลักษณะของ Yield Curve ได้แก่ VIX, Inflation, GDP Growth และ Debt-to-GDP Ratio โดยมีรายละเอียดของสมมติฐานในการศึกษาดังตารางที่ 1
ตารางที่ 1 สมมติฐานในการศึกษา
| ตัวแปร | ความสัมพันธ์กับลักษณะของ Yield Curve |
| VIX | ทิศทางเดียวกันกับความโค้ง |
| Inflation | ทิศทางเดียวกันกับระดับ/ทิศทางตรงกันข้ามกับความชัน |
| GDP Growth | ทิศทางเดียวกันกับระดับและความชัน |
| Debt-to-GDP Ratio | ทิศทางเดียวกันกับระดับและความชัน |
VIX แสดงถึงความผันผวนของตลาดทางการเงิน และสะท้อนความเชื่อมั่นของนักลงทุน จึงนำมาศึกษาความสัมพันธ์กับความโค้ง โดยที่หาก VIX เพิ่มขึ้น หมายความว่าความผันผวนของตลาดมากขึ้น ส่งผลให้ความโค้งมากขึ้นด้วย จึงกล่าวได้ว่า VIX มีความสัมพันธ์ในทิศทางเดียวกันกับความโค้งของ Yield Curve ซึ่งสอดคล้องกับสมมติฐานในการศึกษาของ Hansen (2023)
Inflation แสดงถึงอัตราเงินเฟ้อ โดยหาก Inflation สูงขึ้น นักลงทุนย่อมหวังผลตอบแทนที่สูงขึ้นเพื่อให้ผลตอบแทนที่จะได้รับในอนาคตเพียงพอกับค่าใช้จ่ายที่จะเกิดขึ้น ซึ่งอธิบายได้จาก Expectation Theory ดังนั้น อัตราผลตอบแทนของพันธบัตรจะปรับตัวเพิ่มขึ้น เป็นผลให้ระดับของ Yield Curve เพิ่มขึ้น จึงกล่าวได้ว่า Inflation มีความสัมพันธ์ในทิศทางเดียวกันกับระดับของ Yield Curve อย่างไรก็ตาม เนื่องจากนักลงทุนอาจคาดว่าธนาคารกลางจะเพิ่มอัตราดอกเบี้ยนโยบาย เพื่อลดอัตราเงินเฟ้อ อัตราผลตอบแทนจึงเพิ่มขึ้น ส่งผลให้ระดับของ Yield Curve เพิ่มขึ้นในระยะสั้นเท่านั้น ดังนั้น ความชันของ Yield Curve ในระยะยาวจะลดลง ซึ่งอธิบายได้จากทฤษฎีนโยบายการเงินกับ Yield Curve จึงกล่าวได้ว่า Inflation มีความสัมพันธ์ในทิศทางเดียวกันกับระดับของ Yield Curve ในขณะที่มีความสัมพันธ์ในทิศทางตรงกันข้ามกับความชันของ Yield Curve ซึ่งสอดคล้องกับสมมติฐานในการศึกษาของภารัตตะ (2019)
GDP Growth แสดงถึงกิจกรรมทางเศรษฐกิจ เมื่อ GDP Growth เพิ่มขึ้น หมายความว่าประเทศมีการผลิตเพิ่มขึ้น เศรษฐกิจของประเทศเกิดการขยายตัว อัตราดอกเบี้ยสูงขึ้น ซึ่งอธิบายได้จาก Expectation Theory ดังนั้น อัตราผลตอบแทนของพันธบัตรจะปรับตัวเพิ่มขึ้น เป็นผลให้ระดับและความชันของ Yield Curve เพิ่มขึ้น จึงกล่าวได้ว่า GDP Growth มีความสัมพันธ์ในทิศทางเดียวกันกับระดับและความชันของ Yield Curve ซึ่งสอดคล้องกับสมมติฐานในการศึกษาของภารัตตะ (2019)
Debt-to-GDP Ratio แสดงถึงนโยบายการคลัง หากดำเนินนโยบายการคลังแบบขยายตัวโดยการเพิ่มรายจ่ายภาครัฐและการก่อหนี้สาธารณะเพิ่มขึ้น คาดว่าจะส่งผลให้ความชันของเส้นอัตราผลตอบแทนสูงขึ้น เนื่องจากนโยบายการคลังแบบขยายตัวจะเพิ่มความคาดหวังต่ออัตราเงินเฟ้อในระยะยาว นักลงทุนจึงต้องการผลตอบแทนที่มากขึ้นในช่วงปลายเส้นอัตราผลตอบแทน เพื่อชดเชยมูลค่าของเงินที่ลดลง ดังนั้น เมื่อ Debt-to-GDP Ratio สูงขึ้น หมายถึงความต้องการเงินกู้ของภาครัฐที่เพิ่มสูงขึ้น จึงมีแนวโน้มที่ภาครัฐจะเพิ่มอุปทานพันธบัตรรัฐบาลในตลาด ในขณะที่อุปสงค์พันธบัตรรัฐบาลคงเดิม ทำให้ราคาพันธบัตรถูกลง อัตราผลตอบแทนสูงขึ้น เป็นผลให้ระดับและความชันของ Yield Curve สูงขึ้น โดยเฉพาะในระยะยาว เนื่องจากความล่าช้าของโครงการภาครัฐ จึงกล่าวได้ว่า Debt-to-GDP Ratio มีความสัมพันธ์ในทิศทางเดียวกันกับระดับและความชันของ Yield Curve
กล่าวโดยสรุป สมมติฐานของการศึกษาครั้งนี้คือตัวแปรนโยบายการคลังมีความสัมพันธ์เชิงพลวัตกับลักษณะของ Yield Curve จึงมีการประเมินแบบจำลอง VAR สำหรับชุดข้อมูลของประเทศไทย ดังนี้

แบบจำลอง VAR มีการเรียงลำดับในแบบจำลอง (Ordering) จากตัวแปรภายนอกมากที่สุดไปยังตัวแปรภายนอกน้อยที่สุด และได้ระบุผลกระทบเฉียบพลัน (Shocks) ไว้ในระบบแบบจำลอง โดยอาศัยข้อจำกัดการเรียกซ้ำร่วมสมัยอย่างง่าย (Simple Contemporary Recursive Restrictions) ที่กำหนดโดย Choleski triangular factorization ของเมทริกซ์ความแปรปรวนและความแปรปรวนร่วม ซึ่งมีการสันนิษฐานว่าการเปลี่ยนแปลงทางเศรษฐกิจมหภาค อาจส่งผลกระทบทันทีต่อตัวแปรนโยบายการคลัง แต่การเปลี่ยนแปลงของนโยบายการคลังนั้นไม่มีผลกระทบต่อเศรษฐกิจมหภาคในทันที เนื่องจากความล่าช้าของนโยบายทำให้ตัวแปรนโยบายการคลังอยู่ในตำแหน่งส่วนท้ายในระบบ รวมถึงระดับ ความชัน และความโค้งด้วย
การคำนวณปัจจัยแฝงของ Yield Curve ทั้งสาม จะใช้ Bond Yield อายุครบกำหนดของพันธบัตรรวม 13 รายการ ได้แก่ 1 เดือน, 3 เดือน, 6 เดือน, 12 เดือน, 24 เดือน, 36 เดือน, 48 เดือน, 60 เดือน,72 เดือน, 84 เดือน, 96 เดือน, 108 เดือน และ 120 เดือน โดยกำหนดให้ Bond Yield อายุคงเหลือ 1 เดือน และ 12 เดือนเป็นตัวแทนของพันธบัตรระยะสั้น อัตราผลตอบแทนของพันธบัตรอายุคงเหลือ 48 เดือน เป็นตัวแทนของพันธบัตรระยะกลาง และอัตราผลตอบแทนของพันธบัตรอายุคงเหลือ 84 เดือน และ 120 เดือน เป็นตัวแทนของพันธบัตรระยะยาว เพื่อใช้ในการวิเคราะห์แบบจำลอง VAR สำหรับประเทศไทย โดยมีแบบจำลองจะใช้ข้อมูลตั้งแต่ไตรมาสที่ 1 ปี 2005 ถึงไตรมาสที่ 3 ปี 2023 จำนวน 75 ไตรมาส
4. ผลการศึกษาและอภิปรายผล (Results and Discussion)
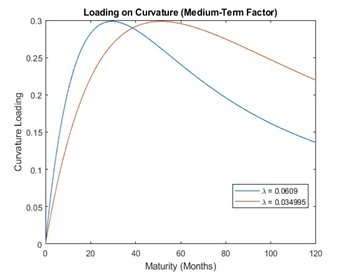
ขั้นตอนในการหาปัจจัยแฝงระดับ ความชัน และความโค้ง เริ่มต้นจากการหาค่าประมาณของ โดยที่แบบจำลอง Nelson-Siegel ได้ตั้งค่า เท่ากับ 0.0609 ความโค้งสูงสุดอยู่ที่ 30 เดือน ซึ่งการศึกษาครั้งนี้ได้ค่าประมาณ เท่ากับ 0.035 หมายถึงค่าสูงสุดของปัจจัยแฝงในระยะกลางหรือความโค้งที่ระยะเวลาครบกำหนด 48 เดือน ซึ่งมีการเสื่อมถอยของปัจจัยในระยะสั้นที่ค่อนข้างช้า เมื่อเทียบกับการศึกษาของ Diebold et al. (2006) และ Diebold and Li (2006) ซึ่งมีค่าสูงสุดของความโค้งอยู่ที่ 23 และ 29 เดือน ตามลำดับ เนื่องจากในแต่ละประเทศมีการเสื่อมถอยของปัจจัยความโค้งที่แตกต่างกันซึ่งอาจเป็นผลมาจากหลายสาเหตุ เช่น สภาพแวดล้อมด้านอัตราดอกเบี้ย รูปร่างเส้นโค้งอัตราผลตอบแทนความคาดหวังของอัตราเงินเฟ้อ ความเสี่ยงด้านเครดิต สภาพคล่อง รวมถึงความคาดหวังและพฤติกรรมของตลาด และในการศึกษาครั้งนี้ใช้ข้อมูลพันธบัตรที่มีอายุครบกำหนดและช่วงเวลาที่นำข้อมูลมาศึกษาแตกต่างกับ Diebold et al. (2006) และ Diebold and Li (2006) โดยมีรายละเอียดตามรูปภาพที่ 1
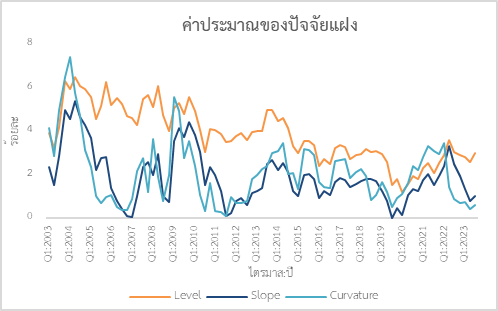
จากรูปภาพที่ 2 แสดงปัจจัยแฝงของ Yield Curve ทั้งสามที่คำนวณด้วย Kalman Smoother หลังจากการลู่เข้าของการประมาณค่าความน่าจะเป็นสูงสุด สามารถสรุปได้ดังนี้
1. ปัจจัยแฝงระดับ แสดงให้เห็นว่าอัตราผลตอบแทนโดยรวมลดลงอย่างต่อเนื่อง เนื่องจากนักลงทุนมีความกังวลเกี่ยวกับความเสี่ยงของการลงทุนในหุ้น จึงมีความต้องการที่จะหันมาลงทุนใน Safe Asset สามารถอนุมานได้ว่าเศรษฐกิจกำลังถดถอยหรืออาจเกิดขึ้นจากหลายปัจจัยที่มีผลต่อตลาดหลักทรัพย์ ซึ่งเป็นปัจจัยสำคัญของเศรษฐกิจและตลาดการเงิน เช่น นโยบายเงินของธนาคารแห่งประเทศไทย โดยการลดอัตราดอกเบี้ยนโยบายอย่างต่อเนื่อง สามารถทำให้ Bond Yield ลดลงตามไปด้วย หรือแม้กระทั่งเหตุการณ์ที่เกิดขึ้นทั่วโลก เช่น สงครามทางการค้า วิกฤตทางการเงินและเศรษฐกิจโลก เป็นต้น
2. ปัจจัยแฝงความชัน แสดงให้เห็นว่าความชันของ Yield Curve ประเทศไทยโดยรวมลดลงเป็นส่วนใหญ่ และมีช่วงที่ปัจจัยความชันเข้าใกล้ศูนย์ ได้แก่ ไตรมาสที่ 1 ปี 2007 ไตรมาสที่ 3 ปี 2011 และไตรมาสที่ 3 ปี 2019 อาจเป็นผลมาจากการดำเนินนโยบายการเงินและนโยบายการคลังแบบขยายตัวเพื่อกระตุ้นเศรษฐกิจในช่วงเวลาดังกล่าว ผ่านการลดอัตราดอกเบี้ยนโยบายควบคู่กับการเพิ่มการใช้จ่ายของรัฐ เช่น ในปี 2011 ประเทศไทยเกิดมหาอุทกภัย ส่งผลกระทบต่อภาคอุตสาหกรรมและภาคการท่องเที่ยวอย่างมาก เป็นต้น ซึ่งมีความสอดคล้องกันระหว่างทฤษฎีนโยบายการเงินกับการเปลี่ยนแปลงของ Yield Curve คือหากมีการดำเนินนโยบายการเงินแบบขยายตัว จะส่งผลให้ Yield Curve ในระยะสั้นมีการเปลี่ยนแปลงระดับและความชันลดลง ถึงแม้ว่าความสัมพันธ์ระหว่างทฤษฎีนโยบายการคลังกับการเปลี่ยนแปลงของ Yield Curve จะมีการเปลี่ยนแปลงระดับและความชันเพิ่มขึ้นในระยะยาว เมื่อมีการดำเนินนโยบายการคลังแบบขยายตัว แต่ในขณะเดียวกัน ในช่วงที่เกิดวิกฤติเศรษฐกิจ นักลงทุนจะหันไปซื้อ Safe Asset เช่น หลักทรัพย์กระทรวงการคลังที่มีอายุครบกำหนดชำระในระยะยาว หรือเรียกว่า Flight to Safety การซื้อประเภทนี้เป็นการกดดันอัตราผลตอบแทนในช่วงปลายของ Yield Curve ลดลง
3. ปัจจัยแฝงความโค้ง โดยปกติความโค้งจะมีความแปรผันที่สูงกว่าความชันและระดับค่อนข้างมาก แม้ว่าทั้งระดับ ความชัน และความโค้งของ Yield Curve จะสะท้อนถึงการเปลี่ยนแปลงในสภาวะตลาดและความคาดหวังของนักลงทุน แต่ปัจจัยที่ทำให้เกิดความผันผวนอาจแตกต่างกัน ระดับและความชันนั้นเชื่อมโยงโดยตรงกับการเปลี่ยนแปลงของนโยบายการคลัง ในขณะที่ความโค้งสะท้อนถึงการเปลี่ยนแปลงของความเชื่อมั่นของตลาดและความคาดหวังสำหรับการเคลื่อนไหวของอัตราดอกเบี้ยในอนาคต ซึ่งในกรณีประเทศไทย ความโค้งมีความสัมพันธ์เชิงบวกที่ชัดเจนกับความชันตลอดช่วงเวลาตั้งแต่ไตรมาสที่ 1 ปี 2003 ถึงไตรมาสที่ 3 ปี 2023 อย่างไรก็ตาม จากผลการประมาณค่าในบางช่วงความโค้งมีค่าสูงกว่าความชัน อาจเป็นผลมาจากความคาดหวังทางเศรษฐกิจ และความไม่แน่นอนทางเศรษฐกิจและการเงินเพิ่มสูงขึ้นกว่าผลของการดำเนินนโยบายการคลัง
การวิเคราะห์แบบจำลอง VAR ของนโยบายการคลัง ได้มีการทดสอบคุณสมบัติความนิ่ง (Stationary) หรือ Unit Root Test ของตัวแปรที่นำมาศึกษาด้วยวิธี Augmented Dickey-Fuller Test พบว่าตัวแปรทุกตัวค่า p-value น้อยกว่า 0.05 หมายความว่าข้อมูลตัวแปรทุกตัวมีคุณสมบัติ Stationary ณ ระดับความเชื่อมั่นร้อยละ 95 และได้ทำการเลือก Lag length พบว่า Lag length ที่เหมาะสมในการนำมาวิเคราะห์แบบจำลองเท่ากับ 1 รวมถึงการทดสอบการแจกแจงความโค้งปกติ (Normality Test) และการทดสอบปัญหา Autocorrelation ด้วยวิธี Serial Correlation LM Test ซึ่งจะทำกระบวนการทั้งหมดนี้พบว่า ไม่เกิดปัญหา Autocorrelation ณ ระดับความเชื่อมั่นร้อยละ 95 อย่างไรก็ตาม เนื่องจากค่าสัมประสิทธิ์ที่ได้จากการประมาณค่าแบบจำลอง VAR นั้นยังไม่สามารถอธิบายตัวแปรต่าง ๆ ในแบบจำลองได้อย่างชัดเจน ดังนั้น จึงต้องมีการวิเคราะห์ในรูปแบบอื่นเพื่อให้สามารถอธิบายความสัมพันธ์ของตัวแปรต่าง ๆ ในแบบจำลองได้ดียิ่งขึ้น โดยวิธีที่นำมาใช้คือการวิเคราะห์ Impulse Response Function เพื่อวิเคราะห์การตอบสนองของอัตราผลตอบแทนพันธบัตร เมื่อเกิด Shocks ของตัวแปรต่าง ๆ ในแบบจำลอง และ Variance Decomposition เพื่อวิเคราะห์การตอบสนองต่อ Shocks ของตัวแปรในแบบจำลองว่ามีผลกระทบมาจากการเปลี่ยนแปลงของตัวแปรอื่นเป็นสัดส่วนเท่าใด รวมถึงการทดสอบความเป็นเหตุเป็นผลโดยการใช้ Granger Causality เพื่อให้ได้หลักฐานเชิงประจักษ์ที่แสดงว่าตัวแปรที่สนใจนั้นมีอำนาจการพยากรณ์ต่อกันอย่างไร ซึ่งการศึกษาครั้งนี้ได้มีการกำหนดตัวแปรกระตุ้น (Impulse) ได้แก่ VIX, Inflation, GDP Growth และ Debt-to-GDP Ratio และกำหนดตัวแปรตอบสนอง (Response) ได้แก่ ระดับ ความชัน และความโค้งของ Yield Curve ที่ประมาณค่าด้วย Kalman Filter โดยสามารถสรุปการวิเคราะห์แบบจำลอง ดังนี้
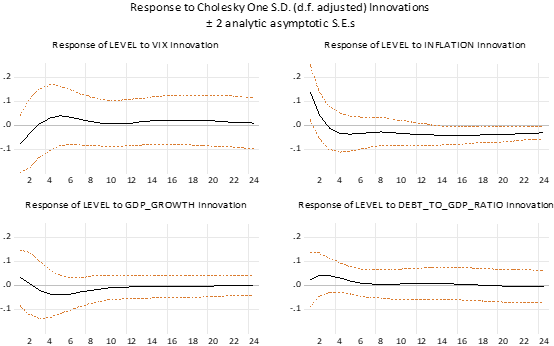
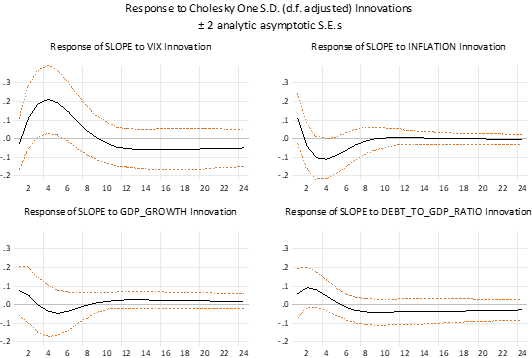
1) การประมาณค่าของ Impulse Response Function ของแบบจำลองนโยบายการคลังที่สอดคล้องกับสมมติฐานในการศึกษา สามารถสรุปได้ดังนี้ (1) Response of Level พบว่า Debt-to-GDP มีผลต่อการเปลี่ยนแปลงของระดับเพิ่มขึ้นในไตรมาสที่ 1 – 2 และค่อย ๆ ลดลงกลับเข้าสู่ค่าปกติในไตรมาสที่ 8 และ (2) Response of Slope พบว่า Debt-to-GDP มีผลต่อการเปลี่ยนแปลงของความชันเพิ่มขึ้นในไตรมาสที่ 1 – 2 และกลับเข้าสู่ค่าปกติในไตรมาสที่ 5
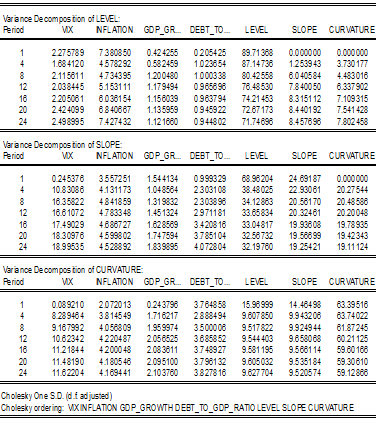
2) การประมาณค่า Variance Decomposition ระหว่างตัวแปร Response กับตัวแปร Impulse ของแบบจำลองนโยบายการคลังตามสมมติฐานของการศึกษา สามารถสรุปได้ดังนี้ (1) Variance Decomposition of Level พบว่าในไตรมาสที่ 8 Debt-to-GDP Ratio สามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของระดับได้ร้อยละ 1.000 อย่างไรก็ตาม เมื่อเวลาผ่านไป Debt-to-GDP Ratio สามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของระดับลดลง (2) Variance Decomposition of Slope พบว่าในไตรมาสที่ 8 Debt-to-GDP Ratio สามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของความชันได้ร้อยละ 2.303 และเมื่อเวลาผ่านไป Debt-to-GDP Ratio สามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของความชันเพิ่มขึ้น
3) การทดสอบ Granger causality ณ ระดับความเชื่อมั่นร้อยละ 95 พบว่ามีเพียง Inflationที่มี Granger-cause ต่อการเปลี่ยนแปลงปัจจัยแฝงระดับและความชัน ในขณะที่ไม่มีตัวแปรใดที่มี Granger-cause ต่อการเปลี่ยนแปลงความโค้ง
จากผลการประมาณค่าจะเห็นได้ว่า Debt-to-GDP Ratio สามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของระดับและความชันได้ค่อนข้างน้อย เมื่อเทียบกับการศึกษาของ António Afonso and Manuel M.F. Martins (2012) ในไตรมาสที่ 8 Debt-to-GDP Ratio ของสหรัฐสามารถอธิบายการเปลี่ยนแปลงของความแปรปรวนของระดับและความชันได้ถึงร้อยละ 15.901 อาจเป็นผลมาจากความแตกต่างของขนาดหรือลักษณะของตลาดตราสารหนี้ระหว่างไทยกับสหรัฐ รวมถึงจำนวนข้อมูลที่ใช้ในการวิเคราะห์แบบจำลองมีความแตกต่างกัน
5. สรุปผลการศึกษาและข้อเสนอแนะ (Conclusion and Policy Implication)
การศึกษาในครั้งนี้เป็นการศึกษาเกี่ยวกับลักษณะของ Yield Curve ประกอบด้วย ระดับ ความชัน และความโค้ง ซึ่งลักษณะของ Yield Curve นั้นจะวัดโดยการประมาณการของระดับ ความชัน และความโค้ง ของแบบจำลอง Nelson and Siegel (1987) และการประมาณค่า Maximum Likelihood ด้วย Kalman Filter ที่แนะนำโดย Diebold and Li (2006) และ Diebold, Rudebusch and Aruoba (2006) และเพื่อศึกษาความสัมพันธ์เชิงพลวัตระหว่างลักษณะของ Yield Curve กับนโยบายการคลังของประเทศไทย ซึ่งจากผลการประมาณค่า Impulse Response Function สามารถสรุปผลการศึกษาได้ดังนี้ (1) VIX มีผลต่อการเปลี่ยนแปลงความโค้งในทิศทางเดียวกัน โดยที่การศึกษาอื่น ๆ มักจะพบว่า ไม่มีปัจจัยใดที่ส่งผลต่อความโค้ง แต่ได้มีการอธิบายถึงความไม่แน่นอนของตลาดและความเชื่อมั่นของนักลงทุนอาจส่งผลต่อความโค้ง ผู้ศึกษาจึงได้ศึกษาเกี่ยวกับความสัมพันธ์ระหว่าง VIX และความโค้งของ Yield Curve (2) Inflation ส่งผลกระทบต่อระดับและความชันในทิศทางเดียวกัน ซึ่งการที่ Inflation ส่งผลกระทบต่อระดับในทิศทางเดียวกันสอดคล้องกับ Expectation Theory ในขณะที่ Inflation ส่งผลกระทบต่อความชันในทิศทางเดียวกันนั้นไม่สอดคล้องกับทฤษฎีและสมมติฐานในการศึกษา อย่างไรก็ตาม ยังมีการศึกษาที่พบว่า Inflation ส่งผลกระทบต่อความชันในทิศทางเดียวกัน โดยได้อธิบายว่าอัตราผลตอบแทนจะเพิ่มขึ้นในอัตราเดียวกันกับอัตราเงินเฟ้อที่คาดว่าจะเกิดขึ้นในประเทศจีน (Johansson, 2010) นอกจากนี้ อาจเป็นผลมากจากการที่อัตราเงินเฟ้อสูงขึ้น ทำให้ธนาคารแห่งประเทศไทยเพิ่มอัตราดอกเบี้ยนโยบาย ทำให้อัตราผลตอบแทนระยะสั้นเพิ่มขึ้น อีกทั้งนักลงทุนก็จะคาดการณ์ว่าอัตราดอกเบี้ยจะเพิ่มขึ้นอย่างต่อเนื่อง ส่งผลให้อัตราผลตอบแทนพันธบัตรระยะยาวเพิ่มขึ้นมากกว่าอัตราผลตอบแทนพันธบัตรระยะสั้นที่เพิ่มขึ้น ทำให้ความชันของ Yield Curve เพิ่มขึ้นซึ่งแต่ละประเทศอาจมีการตอบสนองของ Yield Curve ต่ออัตราเงินเฟ้อที่แตกต่างกัน (3) GDP Growth ส่งผลกระทบต่อระดับและความชันในทิศทางเดียวกันสอดคล้องกับสมมติฐานในการศึกษา และ (4) Debt-to-GDP ส่งผลกระทบต่อระดับและความชันในทิศทางเดียวกัน ซึ่งสอดคล้องกับทฤษฎี สมมติฐานในการศึกษา และผลการศึกษาอื่น ๆ ที่เกี่ยวข้อง อาทิ António Afonso and Manuel M.F. Martins, 2012
ผลการศึกษาของการดำเนินนโยบายการคลังส่งผลต่อลักษณะของ Yield Curve ประเทศไทย ยังไม่มีความชัดเจนมากนัก เมื่อเทียบกับกรณีศึกษาของสหรัฐและประเทศในยุโรป อาจเป็นผลมาจากความถี่ของข้อมูลที่มีจำกัด อีกทั้งอาจเป็นผลมาจากตลาดทางการเงิน ตลาดตราสารหนี้ รวมถึงตลาดหุ้นของไทย ที่มีขนาดเล็กกว่าสหรัฐและประเทศในยุโรปอยู่ค่อนข้างมาก อย่างไรก็ตาม ความสัมพันธ์ระหว่างการดำเนินนโยบายการคลังกับลักษณะของ Yield Curve ประเทศไทย ยังคงมีความสำคัญมากขึ้นอย่างต่อเนื่อง จะเห็นได้จากเมื่อเวลาผ่านไปแนวโน้มของการเปลี่ยนแปลงนโยบายการคลังสามารถอธิบายการเปลี่ยนแปลงลักษณะของ Yield Curve ได้มากขึ้น ดังนั้น การศึกษาครั้งนี้ทำให้ได้เห็นความสำคัญและแนวโน้มของการดำเนินนโยบายการคลังที่มีผลต่อลักษณะของ Yield Curve มากยิ่งขึ้น
การเปลี่ยนแปลงลักษณะของ Yield Curve มีความสำคัญอย่างมากต่อการคาดการณ์ภาวะเศรษฐกิจในอนาคต โดยที่ Normal Yield Curve มักจะบ่งบอกถึงเศรษฐกิจที่ขยายตัวได้อย่างต่อเนื่อง ในขณะที่ Flat Yield Curve หรือ Inverted Yield Curve บ่งบอกถึงภาวะเศรษฐกิจที่อาจหดตัว รัฐบาลจึงควรมีแนวทางการดำเนินนโยบายการคลังด้วยเครื่องมือต่าง ๆ เนื่องจากผลการศึกษาในครั้งนี้พบว่าเมื่อ Debt-to-GDP Ratio เพิ่มขึ้นส่งผลให้ระดับและความชันของ Yield Curve เพิ่มขึ้น จึงควรให้มีการเพิ่มการลงทุนภาครัฐ เช่นการลงทุนในโครงสร้างพื้นฐานต่าง ๆ จะช่วยเพิ่มการสร้างงาน และกระตุ้นการบริโภคภายในประเทศซึ่งเป็นการเพิ่มอุปสงค์รวม และช่วยสนับสนุนการเติบโตของเศรษฐกิจในระยะยาว รวมถึงการสร้างความเชื่อมั่นให้กับนักลงทุนต่างชาติ ส่งผลดีต่อเศรษฐกิจในภาพรวม ซึ่งการใช้เครื่องมือและนโยบายต่าง ๆ เหล่านี้ รัฐบาลอาจจะสามารถทำให้ Yield Curve ของไทยเปลี่ยนแปลงจากรูปแบบ Flat Yield Curve กลับมาสู่ Normal Yield Curve ได้ ซึ่งจะส่งสัญญาณที่ดีต่อเศรษฐกิจและเพิ่มความเชื่อมั่นให้กับนักลงทุนและประชาชน
ในประเทศ
บรรณานุกรม
Adam Kucera, E. K. (2019). Yield Curve Dynamics and Fiscal Policy Shocks. Working paper NBS, 1-40.
Aeimit Lakdawala, B. P. (2023). Impact of RBI’s monetary policy announcements on government bond yields: evidence from the pandemic. Indian Economic Review, 261-291.
Alexander W. Hoffmaister, J. R. (2010). Yield Curve Dynamics and Spillovers in Central and Eastern European Countries . IMF Working Paper, 1-60.
Anne Lundgaard Hansen. (2023). Predicting recessions using VIX–yield curve cycles. International Journal of Forecasting.
Asia Regional Integration Center. (2023, October 6). Financial Stress Index. Retrieved from www.aric.adb.org: https://aric.adb.org/database/fsi
Benati, C. B. (2013). Unconventional Monetary Policy and the Great Recession: Estimating the Macroeconomic Effects of a Spread Compression at the Zero Lower Bound. International Journal of Central Banking, 165-212.
CEIC. (2023, November 10). Consumer Price Index. Retrieved from www.info.ceicdata.com.
Chernov, R. B. (2010). No-arbitrage macroeconomic determinants of the yield curve. Journal of Econometrics, 166-182.
Christane Nickel, P. C. (2009). FISCAL VARIABLES AND BOND SPREADS – EVIDENCE FROM EASTERN EUROPEAN COUNTRIES AND TURKEY. European Central Bank Working Paper Series No. 1101, 1-45.
Francis X. Diebold, G. D. (2004). THE MACROECONOMY AND THE YIELD CURVE: A DYNAMIC LATENT FACTOR APPROACH. NBER WORKING PAPER, 1-40.
Giglio, C. A. (2006). Fiscal Policy and the Term Structure: Evidence from the Case of Italy in the EMS and the EMU Periods. Working Paper of Innocenzo Gasparni Institute for Economic Research, 1-39.
Goyal, K. K. (2002). Yield Spread as a Lead Indicator of Real Economic Activity: An Empirical Exercise on the Indian Economy. Economic and Political Weekly, 3670 – 3676.
Hans Dewachter and Marco Lyrio. (2006). Macro Factors and the Term Structure of Interest Rates. Journal of Money, Credit and Banking, 119-140.
Jan Annaert, A. G. (2013). Estimating the spot rate curve using the Nelson–Siegel model. International Review of Economics and Finance, 482-496.
King, M. B. (1993). Fiscal Policy in General Equilibrium. The American Economic Review, 315-334.
Kozicki, S. (1997). Predicting Real Growth and Inflation with the Yield Spread. FEDERAL RESERVE BANK OF KANSAS CITY, 39-57.
Kris Piroj. (24 ธันวาคม 2022). Crowding out Effect คืออะไร? เกิดขึ้นได้อย่างไร. เข้าถึงได้จาก GreedisGoods: https://greedisgoods.com/crowding-out-effect/
Li, F. X. (2003). FORECASTING THE TERM STRUCTURE OF GOVERNMENT BOND YIELDS. NBER WORKING PAPER, 1-43.
Li, F. X. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 337-364.
Longzhen Fan and Anders C. Johansson. (2010). China’s official rates and bond yields. Journal of Banking & Finance, 996-1007.
Maria-Grazia Attinasi, C. C. (2009). WHAT EXPLAINS THE SURGE IN EURO AREA SOVEREIGN SPREADS DURING THE FINANCIAL CRISIS OF 2007-09? European Central Bank Working Paper Series No. 1131, 1-49.
Martins, A. A. (2012). Level, slope, curvature of the sovereign yield curve, and fiscal behaviour. Journal of Banking & Finance, 1789-1807.
Mishkin, A. E. (1996). The yield curve as a predictor of recessions in the United States and Europe. Bank for International Settlement, 324-339.
Nguyen, T. M. (2014). THE YIELD CURVE AS A LEADING INDICATOR ACROSS . Honors Theses and Capstones, 208.
Pereira, H. O. (2013). Yield Curve as a Predictor of Recessions: Evidence from Panel Data. Emerging Markets Finance & Trade, 194-212.
Pond, G. J. (2019). U.S. MONETARY POLICY TRANSMISSION: THE YIELD CURVE AND ECONOMIC ACTIVITY IN THE U.S. AND ABROAD. A Thesis Presented to the faculty of the Department of Economics California State University, Sacramento, 1-75.
Rault, A. A. (2010). Long-run Determinants of Sovereign Yields. CESIFO WORKING PAPER NO. 3155, 1-13.
Rimal, S. (2021). TESTING THE PREDICTIVE POWER OF TERM . Jyväskylä University, 1-61.
Salvador Barrios, P. I. (2009). Determinants of intra-euro area government bond spreads during the financial crisis. Economic Papers of Economic and Financial Affairs, 1-26.
Scheinkman, R. L. (1991). Common Factors Affecting Bond Returns. The Journal of Fixed Income, 54-61.
Schunk, J. G. (2002). Predicting Regional Recessions Via the Yield Spread. The Review of Regional Studies, 151-170.
Siegel, C. R. (1987). Parsimonious Modeling of Yield Curves. The Journal of Business , 473-489.
TAKEDA, Y. S. (2000). Predicting the US Real GDP Growth Using Yield Spread of Corporate Bonds. International Department Working Paper, 1-25.
ThaiBMA. (2023, November 24). Government Bond Yield Curve. Retrieved from www.thaibma.or.th: https://www.thaibma.or.th/EN/Market/YieldCurve/Government.aspx
ThaiBMA. (24 พฤศจิกายน 2566). เครื่องมือวิเคราะห์การลงทุนในตราสารหนี้เบื้องต้น. เข้าถึงได้จาก www.thaibma.or.th: https://www.thaibma.or.th/EN/Education/Bond_Blog/Tool.aspx
Turnovsky, W. H. (1992). Fiscal Policy and the Term Structure of Interest Rates: An Intertemporal Optimizing Analysis. Journal of Money, Credit and Banking, 1-26.
Williams, G. D. (2007). Forecasting Recessions: The Puzzle of the Enduring Power of the Yield Curve . FEDERAL RESERVE BANK OF SAN FRANCISCO , 1-31.
Wincoop, C. T. (2010). International capital flows. Journal of International Economics, 157-175.
Wolswijk, S. M. (2009). What Drives Spreads in the Euro Area Government Bond Market? Economic Policy, 191-240.
Zhe Huang. (2021). Fitting Yield Curve with Dynamic Nelson-Siegel Models: Evidence from Sweden. Uppsala: Uppsala Universitet.
Zoli, S. S. (2009). Euro Area Sovereign Risk During the Crisis. International Monetary Fund Working Paper , 1-25.
ธนวัฒน์ คงสุวรรณ์. (2563). การใช้ส่วนต่างผลตอบแทนพันธบัตรรัฐบาลเป็นเครื่องชี้นำภาวะเศรษฐกิจของประเทศไทย. สถาบันบัณฑิตพัฒนบริหารศาสตร์, 1-45.
ธนาคารแห่งประเทศไทย. (6 ตุลาคม 2566). สถิติตลาดการเงิน. เข้าถึงได้จาก www.bot.or.th: https://www.bot.or.th/th/statistics/financial-market-statistics.html
ธนาคารแห่งประเทศไทย. (ม.ป.ป.). FM_RT_001_S2 อัตราดอกเบี้ยในตลาดเงิน (2548-ปัจจุบัน). เข้าถึงได้จาก https://app.bot.or.th: https://app.bot.or.th/BTWS_STAT/statistics/BOTWEBSTAT.aspx?reportID=223&language=TH
นลพรรณ มณีโชติ และพีระ ตั้งธรรมรักษ์. (2566). ปัจจัยที่ส่งผลต่อ 2-10 Spread ประเทศไทย. วารสารธุรกิจปริทัศน์, 127-154.
ปัณฑ์ชลิตา ภารัตตะ. (2019). ความสัมพันธ์ระหว่างตัวแปรในระบบเศรษฐกิจกับรูปร่างของเส้นอัตราผลตอบแทน. เข้าถึงได้จาก สถาบันบัณฑิตพัฒนบริหารศาสตร์: https://econ.nida.ac.th/wp-content/uploads/2019/08/6010322020.pdf
ฝ่ายพัฒนาความรู้ผู้ประกอบวิชาชีพ . (2564). การวิเคราะห์การลงทุนในตราสารหนี้. กรุงเทพมหานคร: ตลาดหลักทรัพย์แห่งประเทศไทย.
สำนักงานเศรษฐกิจการคลัง. (24 พฤศจิกายน 2566). ข้อมูลสถิติ. เข้าถึงได้จาก www.fpo.go.th: https://www.fpo.go.th/main/Statistic-Database.aspx
สำนักงานบริหารหนี้สาธารณะ. (24 พฤศจิกายน 2023). หนี้สาธารณะ. เข้าถึงได้จาก www.pdmo.go.th: https://www.pdmo.go.th/th/public-debt/debt-outstanding
สำนักงานบริหารหนี้สาธารณะ. (ม.ป.ป.). ข้อมูลหนี้สาธารณะคงค้าง. เข้าถึงได้จาก www.pdmo.go.th: https://www.pdmo.go.th/th/public-debt/debt-outstanding
สำนักงานสภาพัฒนาการเศรษฐกิจและสังคมแห่งชาติ. (9 สิงหาคม 2566). รายงานภาวะเศรษฐกิจไตรมาส. เข้าถึงได้จาก www.nesdc.go.th: https://www.nesdc.go.th/main.php?filename=QGDP_report
อัญญา ขันธวิทย. (2556). ตัวแบบจําลอง Dynamic Nelson-Siegel ไม่ควรนํามาใช้เพื่อการค้าตราสารหนี้ไทย. วารสารการจัดการสมัยใหม, 58-73.
ภาคผนวก
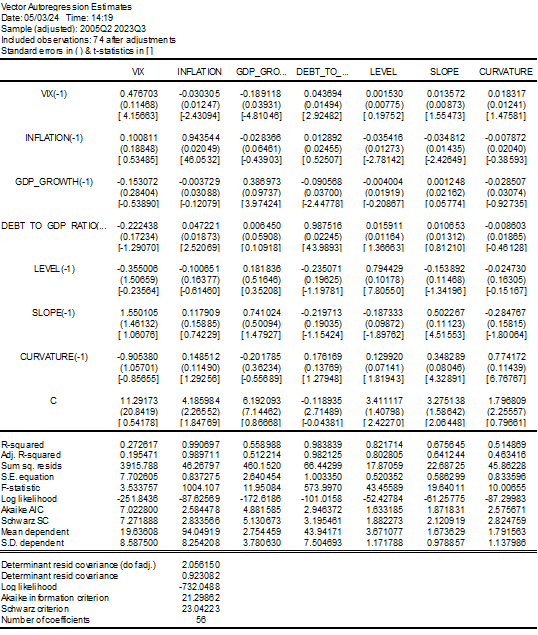
1. ผลการประมาณค่า VAR ของแบบจำลองนโยบายการคลัง
2. Response of Level ของแบบจำลองนโยบายการคลัง
3. Response of Slope ของแบบจำลองนโยบายการคลัง
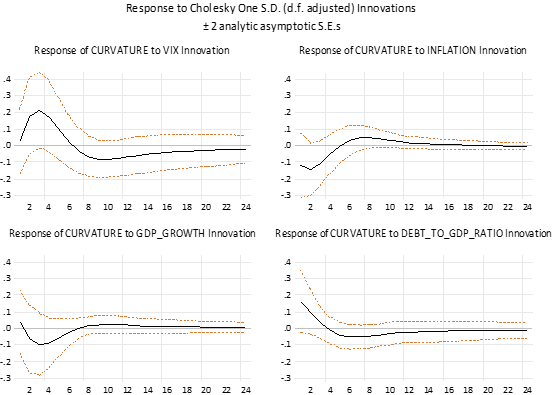
4. Response of Curvature ของแบบจำลองนโยบายการคลัง
5. Variance decomposition ของตัวแปรปัจจัยแฝงกับแบบจำลองของนโยบายการคลัง


นลพรรณ มณีโชติ
เศรษฐกรปฏิบัติการ
ผู้เขียน
